报告现场

陈大岳主持报告并向张益唐颁发“welcome欢迎光临威尼斯公司优秀校友”证书
十年前,孪生素数猜想的一个弱形式被证明了,后来,这个结果被Maynard等人大大改进了,在本次报告中,张益唐简要回顾了相关历史,并总结了证明的思想。Goldston,Pintz和Yildrim在早期工作中,引入素数的特征函数来表示一个数是否为素数。从而,孪生素数猜想——存在无穷多个素数对使得两素数的差为2,即要证明,存在无穷多个n使得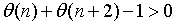 。孪生素数猜想是数论中最为著名的命题之一,是众多数论家的梦想。
。孪生素数猜想是数论中最为著名的命题之一,是众多数论家的梦想。
Goldston等人在经过一系列变式后,转而试图证明孪生素数猜想的弱化版本,试图通过固定一组正整数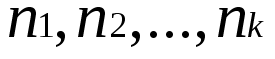 后,寻找非负的一组
后,寻找非负的一组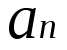 ,使得求和式
,使得求和式

对无穷多个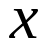 成立,从而实现证明存在无穷多个差被控制在
成立,从而实现证明存在无穷多个差被控制在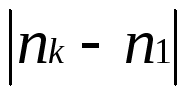 以下的素数对。他们进行了一系列构造,找到了一组
以下的素数对。他们进行了一系列构造,找到了一组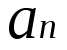 形式为
形式为
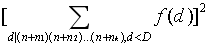
其中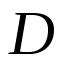 为待定的
为待定的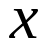 的幂。结合著名的
的幂。结合著名的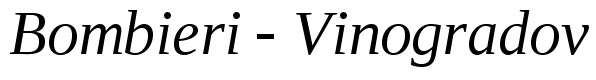 定理,
定理,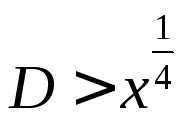 的情形成为最为棘手的部分。
的情形成为最为棘手的部分。
张益唐结合解析数论的各种经典结果,并使用了一些代数几何中的新技术,例如有限域上的黎曼假设,通过在变量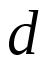 上的限制,成功控制了待证式中的误差项,证明了
上的限制,成功控制了待证式中的误差项,证明了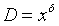 对某些
对某些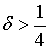 可以使得原命题成立。这在数学界中是一项极大的突破,引起广大数论家的关注,也在之后被用于推进孪生素数猜想的探索。随后,陶哲轩组织了一个线上项目,利用张益唐的结果,寻找素数对之差的最佳结果。到目前为止,已经实现证明差为246的情形。也即,存在无穷多个素数对,使得它们的差不大于246。
可以使得原命题成立。这在数学界中是一项极大的突破,引起广大数论家的关注,也在之后被用于推进孪生素数猜想的探索。随后,陶哲轩组织了一个线上项目,利用张益唐的结果,寻找素数对之差的最佳结果。到目前为止,已经实现证明差为246的情形。也即,存在无穷多个素数对,使得它们的差不大于246。




报告现场
在随后的提问及茶歇环节,参与活动的师生就报告内容及相关的数学问题与张益唐进行了热烈的讨论。



张益唐与师生交流互动

访问期间张益唐与田刚、韦东奕交流